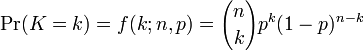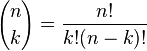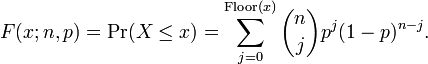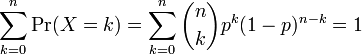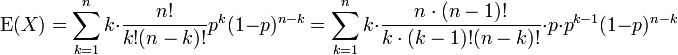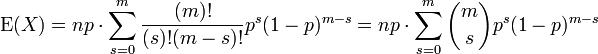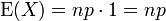큰수의 법칙 시행횟수구하기.pdf

이항 분포

위키백과, 우리 모두의 백과사전.

이항분포
확률 질량 함수

누적 분포 함수
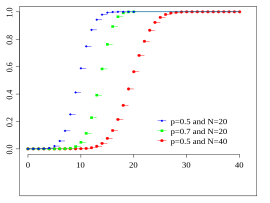Colors match the image above
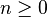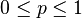매개변수	$n \geq 0$ 시행 횟수 (정수) $0\leq p \leq 1$ 발생 확률 (실수)
지지집합	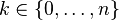$k \in \{0,\dots,n\}\!$
확률 질량	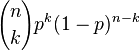${n\choose k} p^k (1-p)^{n-k} \!$
누적 분포	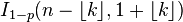$I_{1-p}(n-\lfloor k\rfloor, 1+\lfloor k\rfloor) \!$
기댓값	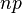$np\!$
중앙값	one of 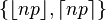$\{\lfloor np\rfloor, \lceil np \rceil\}$ ^[1]
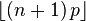최빈값	$\lfloor (n+1)\,p\rfloor\!$
분산	$np(1-p)\!$
비대칭도	$\frac{1-2p}{\sqrt{np(1-p)}}\!$
첨도	$\frac{1-6p(1-p)}{np(1-p)}\!$
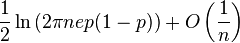엔트로피	$\frac{1}{2} \ln \left( 2 \pi n e p (1-p) \right) + O \left( \frac{1}{n} \right)$
모멘트생성함수	$(1-p + pe^t)^n \!$
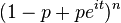특성함수	$(1-p + pe^{it})^n \!$

이항 분포(二項分布)는 연속된 n번의 독립적 시행에서 각 시행이 확률 p를 가질 때의 이산 확률 분포이다. 이러한 시행은 베르누이 시행이라고 불리기도 한다. 사실, n=1일 때 이항 분포는 베르누이 분포이다.

이항 분포는 양봉 분포(Bimodal distribution)와는 다른 것이다.

예[편집]

기본적인 예: 일반적인 주사위를 10회 던져서 숫자 6이 나오는 횟수를 센다. 이 분포는 n = 10이고 p = 1/6인 이항분포이다.

다른 예로는, 아주 많은 인구의 5%가 쌍꺼풀이 있다고 해보자. 그리고 100명을 무작위적으로 선택한다. 당신이 선택한 쌍꺼풀을 가진 사람의 수는 n = 100이고 p = 0.05인 이항분포를 따른다.

상세내용[편집]

ㅣㅣㅣ

확률 질량 함수[편집]

일반적으로, 확률변수 K가 매개변수 n과 p를 가지는 이항분포를 따른다면, K ~ B(n,p)라고 쓴다. n번 시행 중에 k번 성공할 확률은 확률 질량 함수로 주어진다:

\Pr(K = k) = f(k;n,p)={n\choose k}p^k(1-p)^{n-k}

이 때, k = 0, 1, 2, ..., n 이고,

{n\choose k}=\frac{n!}{k!(n-k)!}

는 이항 계수(C(n,k) 또는 nCk라고 쓰기도 함)이다. 이 식은 다음과 같이 이해할 수 있다: 우리는 k번의 성공(p^k)과 n − k번의 실패((1 − p)^n − k)를 원한다. 그러나, k번의 성공은 n번의 시도 중 어디서든지 발생할 수 있고, 또한 k번의 성공을 가지는 분포는 C(n, k)개가 있다.

이항 분포 확률에 대한 참고표를 만들 때, 표는 대체로 n/2개의 값으로 채워져 있다. 이것은 k > n/2에 대해 확률이 다음과 같이 계산될 수 있기 때문이다.

f(k;n,p)=f(n-k;n,1-p).\,\!

그러므로 다른 k와 다른 p를 보아야 한다(이항 분포는 일반적으로 대칭적이지 않음).

누적 분포 함수[편집]

누적 분포 함수는 다음과 같이 베타함수꼴로 쓸 수 있다:

F(k;n,p) = \Pr(X \le k) = I_{1-p}(n-k, k+1) \!

이 때, k는 정수이고, 0 ≤ k ≤ n이다. 만약 x가 정수일 필요가 없거나 양수일 필요가 없다면 다음과 같이 쓸 수 있다:

F(x;n,p) = \Pr(X \le x) = \sum_{j=0}^{\operatorname{Floor}(x)} {n\choose j}p^j(1-p)^{n-j}.

k ≤ np를 만족하는 k에 대해 에 대해 분포 함수의 낮은 꼬리에 대한 상계를 유도할 수 있다. 특히, 호에프딩 부등식을 이용하면 다음을 얻는다:

F(k;n,p) \leq \exp\left(-2 \frac{(np-k)^2}{n}\right), \!

그리고 체르노프 부등식은 다음의 경계를 유도하는 데 사용할 수 있다:

F(k;n,p) \leq \exp\left(-\frac{1}{2\,p} \frac{(np-k)^2}{n}\right). \!

평균, 분산, 최빈값[편집]

만약 X ~ B(n, p)라면, X의 기댓값은

\operatorname{E}(X)=np\,\!

이고 분산은

\operatorname{Var}(X)=np(1-p).\,\!

이것은 쉽게 증명할 수 있다. 먼저 한 번의 베르누이 시행을 생각해보자. 결과는 1과 0 두 가지이고, 1이 나올 확률이 p, 0이 나올 확률이 1 − p이다. 이 시행의 평균은 μ = p이다. 분산의 정의 를 이용하면 다음을 얻는다.

\sigma^2= \left(1 - p\right)^2p + (0-p)^2(1 - p) = p(1-p).

이제 n번의 시행에 대한 분산을 구한다고 생각해보자(일반적인 이항 분포). 각 시행은 독립이므로, 각 시행에 대한 분산들을 더하면

\sigma^2_n = \sum_{k=1}^n \sigma^2 = np(1 - p). \quad

X의 최빈값은 (n + 1)p와 같거나 작은 가장 큰 정수이다; 만약 m = (n + 1)p이 정수라면, m − 1과 m이 둘 다 최빈값이다.

평균과 분산의 명확한 유도[편집]

명확한 유도를 위해 다음의 식을 이용한다.

\sum_{k=0}^n \operatorname{Pr}(X=k) = \sum_{k=0}^n {n\choose k}p^k(1-p)^{n-k} = 1

평균[편집]

먼저, 기댓값의 정의를 적용하면

\operatorname{E}(X) = \sum_k x_k \cdot \operatorname{Pr}(x_k) = \sum_{k=0}^n k \cdot \operatorname{Pr}(X=k) = \sum_{k=0}^n k \cdot {n\choose k}p^k(1-p)^{n-k}

k가 0이므로 첫 번째 항(k' = 0)은 0이다. 이것은 제외될 수 있으므로, 하한을 k = 1로 바꿀 수 있다.

\operatorname{E}(X) = \sum_{k=1}^n k \cdot \frac{n!}{k!(n-k)!} p^k(1-p)^{n-k} = \sum_{k=1}^n k \cdot \frac{n\cdot(n-1)!}{k\cdot(k-1)!(n-k)!} \cdot p \cdot p^{k-1}(1-p)^{n-k}

우리는 n과 k를 팩토리알로부터 꺼냈고, p를 하나 빼냈다.

\operatorname{E}(X) = np \cdot \sum_{k=1}^n \frac{(n-1)!}{(k-1)!(n-k)!} p^{k-1}(1-p)^{n-k}

여기서 m = n - 1 이고, s = k - 1라고 하자.

\operatorname{E}(X) = np \cdot \sum_{s=0}^m \frac{(m)!}{(s)!(m-s)!} p^s(1-p)^{m-s} = np \cdot \sum_{s=0}^m {m\choose s} p^s(1-p)^{m-s}

이 합은 전체 이항 분포에 대한 합이다. 그러므로

\operatorname{E}(X) = np \cdot 1 = np

분산[편집]

분산을 다음과 같이 쓸 수 있다는 것은 증명할 수 있다:

\operatorname{Var}(X) = \operatorname{E}(X^2) - (\operatorname{E}(X))^2.

이 식을 사용하면 X²의 기댓값 역시 필요하다는 것을 알 수 있다. 이것은 다음과 같이 구할 수 있다.

\operatorname{E}(X^2) = \sum_{k=0}^n k^2 \cdot \operatorname{Pr}(X=k) = \sum_{k=0}^n k^2 \cdot {n\choose k}p^k(1-p)^{n-k}.

이를 이용해 계산하면,

\operatorname{E}(X^2) = np \cdot \sum_{s=0}^m k \cdot {m\choose s} p^s(1-p)^{m-s} = np \cdot \sum_{s=0}^m (s+1) \cdot {m\choose s} p^s(1-p)^{m-s}

(마찬가지로, m = n - 1 이고, s = k - 1로 치환). 합을 두 부분으로 나누면,

\operatorname{E}(X^2) = np \cdot \bigg( \sum_{s=0}^m s \cdot {m\choose s} p^s(1-p)^{m-s} + \sum_{s=0}^m 1 \cdot {m\choose s} p^s(1-p)^{m-s} \bigg).

첫 번째 항은 위에서 계산한 평균과 같다. 결과는 mp이다. 두 번째 항은 1이다.

\operatorname{E}(X^2) = np \cdot ( mp + 1) = np((n-1)p + 1) = np(np - p + 1).

이 결과와 평균(E(X) = np)을 이용해서 분산을 다시 표시해보면 다음과 같다.

\operatorname{Var}(X) = \operatorname{E}(X^2) - (\operatorname{E}(X))^2 = np(np - p + 1) - (np)^2 = np(1-p).

주석[편집]

이동↑ Hamza, K. (1995). The smallest uniform upper bound on the distance between the mean and the median of the binomial and Poisson distributions. Statist. Probab. Lett. 23 21–25.

큰수의 법칙(-數-法則)

sonamy | 11.10.27 10:15

큰수의 법칙<law of great numbers>(-數-法則)

경험적 확률과 수학적 확률과의 관계를 나타내는 정리(定理)로서, 대수의 법칙이라고도 한다.

• n개의 사건 중에서 성질 A를 가지는 것이 r개 있으면, r/n는 A가 일어나는 비율로 생각할 수 있는데, 관찰하는 횟수 n을 크게 함에 따라 r/n는 일정한 값 P에 한없이 가까워진다. 이것이 큰수의 법칙이며, 가장 간단한 경우는 ‘베르누이의 정리’에서 설명된다.

• 큰수의 법칙은 확률론에서 발달하여 많은 정리를 탄생시켰다. 이것들을 올바로 이해하려면 엄밀한 정의(定義)에 의존해야 하나, 여기서는 통계에서의 규칙성의 문제로 일반적인 예를 든다. 실제로 나타난 개개의 현상은 우연에 의해 지배되는 일이 많으며, 관찰한 몇 개의 현상 사이에는 아무런 관계가 없는 것처럼 보인다. 그러나 여러 번 관측하고 전체적인 경향을 살펴보면, 거기에서 어떤 일정한 규칙성을 발견할 수 있다.

• 예를 들어 개개인의 수명은 서로 달라 누가 몇 살에 죽을지는 전적으로 불분명하나, 많은 사람에 대해서 장기간에 걸친 통계를 살펴보면 인간의 평균수명, 각 연령층에서의 사망자의 비율이 거의 일정한 값에 가까워지는 것을 알 수 있다. 이런 뜻에서 통계는 모두 어떤 종류의 큰수의 법칙을 나타내고 있다고 할 수 있다.

• 실사회에서 이 법칙을 이용한 전형적인 예는 보험사업이다. 즉, 인간의 수명이나 각 연령별 사망률을 많은 예와 장기간에 걸친 경향에서 구하고, 이것을 기초로 해서 보험금액·보험료율을 계산한다.

출처:http://www.tmath.or.kr/kin/qna/detail.asp?qnaNum=353

저작자표시

'투자의 "정석"' 카테고리의 다른 글

연봉2억 임원_빚 1억__월600사교육비 (0)	2014.09.19
[펌] Excel 엑셀] 절대값 구하기 함수 사용법: Absolute Value Function (0)	2014.09.03
우수성은 기술이 아니라 태도이다._ (0)	2014.09.01
(펌) OECD랭킹 근로시간_한국1위 빼앗김 (0)	2014.08.26
(한방) 1000원짜리 '꼬꼬면'…이경규 "로열티 수억 벌어" (0)	2014.08.25

KEEP CALM AND

(카지노에서, 선물,옵션시장에서) 확률인 아닌 수열로 이기기 위한_큰수의 법칙과 확률분포__확률분포

큰수의 법칙 시행횟수구하기.pdf

이항 분포

목차

예[편집]